A Test Gizmo Element Type
This guide provides another example of the implementation of a new element type. It is not as complete as the one in the How to Create a New Element Type guide, but does illustrate a wider range of network modeling capabilities.
MATPOWER includes implementations of numerous standard element types such as buses, generators, loads, transmission lines, transformers, etc. For this discussion, we use a fictitious element type, a gizmo, that has no physical equivalent, but illustrates a wide range of modeling possibilities. This is element is used in some of the MATPOWER tests to verify custom modeling facilities.
3-Port Gizmo
Let’s say that a gizmo is a 3 port model with 2 non-voltage states. That is, each gizmo connects to 3 different buses and has 2 additional complex state variables, one essentially a current and the other a power flow. And it includes all six types of components that make up the standard AC network model for any element type, as described in the AC Formulations section of the MATPOWER Developer’s Manual.
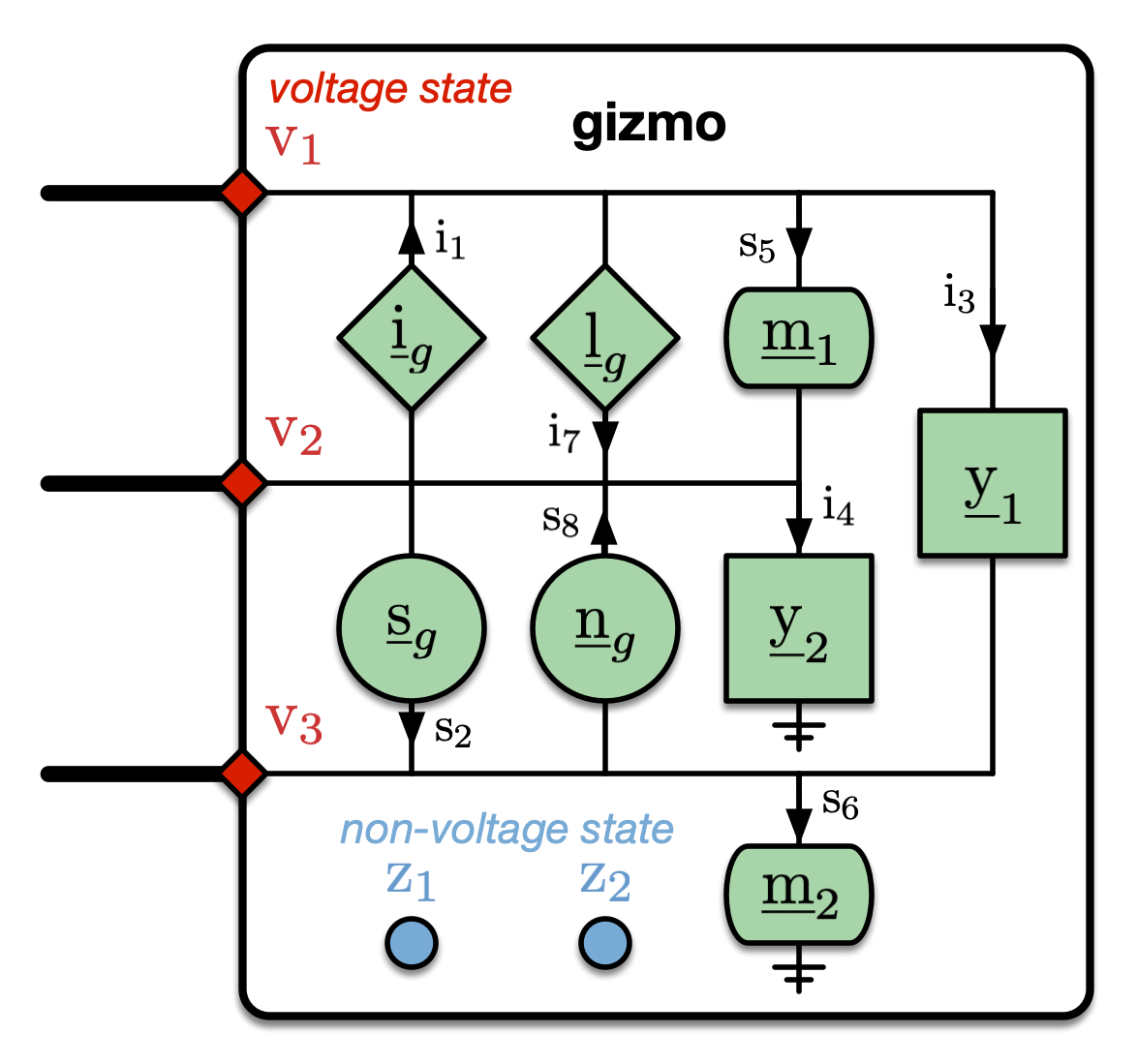
Figure 2 AC Model for 3 Port Gizmo
Figure 2 shows a diagram of the 3-port gizmo, with the various gizmo parameters and the various components summarized in Table 2, with the flows through them as functions of the voltages and non-state variables.
Parameters |
Flow Through This Component |
|---|---|
\(\param{\cscal{i}}_g\) |
complex current is constant |
\(\param{\cscal{s}}_g\) |
complex power is constant |
\(\param{\cscal{y}}_1, \param{\cscal{y}}_2\) |
complex current is proportional to voltage difference (constant impedance) |
\(\param{\cscal{m}}_1, \param{\cscal{m}}_2\) |
complex power is proportional to voltage difference |
\(\param{\cscal{l}}_g\) |
complex current is proportional to non-voltage state |
\(\param{\cscal{n}}_g\) |
complex power is proportional to non-voltage state |
Creating a new element type involves defining and implmementing the corresponding classes for each layer (data, network, and mathematical) of modeling, as well as a corresponding data converter element for each data format. Each of these classes has a name() method that returns the same value, linking them to one another and together defining the gizmo element type. That is, in each type of element class, you will see the following method defined.
function name = name(obj)
name = 'gizmo';
end
Data Model Element
We begin with the data model element for a gizmo. The data for each gizmo consists of the three buses to which its ports are connected, values of the two non-voltage states, and the 8 parameters shown in Figure 2 and Table 2 above. For the complex values, we specify the real and imaginary parts as separate parameters.
This data is stored in the main data table in the tab property of the data model element object of type mp.dme_gizmo. This is a MATLAB table object, or an mp_table object if running in Octave. The names of the columns in tab are shown in Table 3 below. Each row in tab corresponds to an individual gizmo, which means there is a single instance of a gizmo data model element object to hold the data for all gizmos in the system.
Column Names |
Description |
|---|---|
|
bus numbers for the port 1, 2, and 3 connections, respectively |
|
real and imaginary parts of parameters \(\param{\cscal{y}}_1\) and \(\param{\cscal{y}}_2\), respectively |
|
real and imaginary parts of parameters \(\param{\cscal{m}}_1\) and \(\param{\cscal{m}}_2\), respectively |
|
real and imaginary parts of parameter \(\param{\cscal{l}}_g\) |
|
real and imaginary parts of parameter \(\param{\cscal{i}}_g\) |
|
real and imaginary parts of parameter \(\param{\cscal{n}}_g\) |
|
real and imaginary parts of parameter \(\param{\cscal{s}}_g\) |
|
real and imaginary parts of non-voltage state variables \(\cscal{z}_1\) and \(\cscal{z}_2\), respectively |
Listing 15 shows the source code for mp.dme_gizmo. The first thing to notice is that, as with all data model element classes, it inherits from mp.dm_element. Please see the mp.dm_element reference documentation for an overview of the functionality provided and for more details on the methods overridden by mp.dme_gizmo.
1classdef dme_gizmo < mp.dm_element
2 properties
3 bus1 %% bus index vector for port 1
4 bus2 %% bus index vector for port 2
5 bus3 %% bus index vector for port 3
6 end %% properties
7
8 methods
9 function name = name(obj)
10 name = 'gizmo';
11 end
12
13 function label = label(obj)
14 label = 'Test Gizmo';
15 end
16
17 function label = labels(obj)
18 label = 'Test Gizmos';
19 end
20
21 function name = cxn_type(obj)
22 name = 'bus';
23 end
24
25 function name = cxn_idx_prop(obj)
26 name = {'bus1', 'bus2', 'bus3'};
27 end
28
29 function names = main_table_var_names(obj)
30 names = horzcat( main_table_var_names@mp.dm_element(obj), ...
31 {'bus_1', 'bus_2', 'bus_3', 'Y1r', 'Y1i', 'Y2r', 'Y2i', ...
32 'Lr', 'Li', 'Ir', 'Ii', 'M1r', 'M1i', 'M2r', 'M2i', ...
33 'Nr', 'Ni', 'Sr', 'Si', 'Zr1', 'Zi1', 'Zr2', 'Zi2'});
34 end
35
36 function obj = initialize(obj, dm)
37 initialize@mp.dm_element(obj, dm); %% call parent
38
39 %% get bus mapping info
40 b2i = dm.elements.bus.ID2i; %% bus num to idx mapping
41
42 %% set bus index vectors for port connectivity
43 obj.bus1 = b2i(obj.tab.bus_1);
44 obj.bus2 = b2i(obj.tab.bus_2);
45 obj.bus3 = b2i(obj.tab.bus_3);
46 end
47
48 function obj = update_status(obj, dm)
49 %% get bus status info
50 bs = dm.elements.bus.tab.status; %% bus status
51
52 %% update status of gizmoes connected to isolated/offline buses
53 obj.tab.status = obj.tab.status & bs(obj.bus1) & ...
54 bs(obj.bus2) & ...
55 bs(obj.bus3);
56
57 %% call parent to fill in on/off
58 update_status@mp.dm_element(obj, dm);
59 end
60 end %% methods
61end %% classdef
For element types that connect to one or more buses, it is typical to define a property for each port in the data model element class. In our case, there are three properties, bus1, bus2, and bus3, which will hold bus index vectors for ports 1, 2 and 3, respectively. That is dme.bus2(k) will refer to the index of the bus connected to port 2 of the gizmo defined in row k of the data table.
The name() method returns 'gizmo', the name used internally for this element type. The label() and labels() methods provide strings to use for singular and plural user visible labels to use when displaying gizmo elements.
The cxn_type() and cxn_idx_prop() methods specify that 'gizmo' objects connect to 'bus' objects and the corresponding bus indices for ports 1, 2, and 3, can be found in properties bus1, bus2, and bus3, respectively.
The names of the columns in gizmo’s main data table are defined by the return value of main_table_var_names(). Note that it is important to call the parent method to include the column names common to all data model elements (i.e. 'uid', 'name', 'status', 'source_uid').
The initialize() method takes advantage of the bus ID to bus index mapping available from the 'bus' data model element object to populate the bus1, bus2, and bus3 properties from the corresponding columns in the main data table.
Finally, update_status() updates the default online/offline status, which has already been initialized from the status column of the main data table, to remove from service any gizmo that is connected to an offline bus.
Note that both initialize() and update_status() rely on the fact that the corresponding methods have already been called for 'bus' objects before 'gizmo' objects. The order corresponds to their order in dm.element_classes which is determined by the default defined by the data model class and any MATPOWER extensions or options used to modify that default.
The mp.dme_gizmo class is also where you would override any of the pretty-printing methods to implement gizmo sections in your pretty-printed output. Until such methods are added to this example, you can look at the data model element classes for other element types for examples (e.g. mp.dme_bus, mp.dme_branch, mp.dme_gen, mp.dme_load, etc.)
See lib/t/+mp/dme_gizmo.m for the complete mp.dme_gizmo source.
Data Model Converter Element
(not yet documented)
Network Model Element
Next we define the gizmo network model. The focus will be on the AC model with the assumption that both polar and cartesian voltage formulations should be implemented. Because network models are formulation-specific, we will define a class hierarchy for the network model element.
All Formulations
All gizmo network model elements will inherit from mp.nme_gizmo, shown in Listing 16, which in turn inherits from mp.nm_element. Please see the mp.nm_element reference documentation for an overview of the functionality provided and for more details on the methods overridden by mp.nme_gizmo and its subclasses.
1classdef (Abstract) nme_gizmo < mp.nm_element
2 methods
3 function name = name(obj)
4 name = 'gizmo';
5 end
6
7 function np = np(obj)
8 np = 3; %% this is a 3 port element
9 end
10
11 function nz = nz(obj)
12 nz = 2; %% 2 (possibly complex) non-voltage states per element
13 end
14 end %% methods
15end %% classdef
Once again, name() returns the name used internally for this element type, while the np() and nz() methods return the number of ports and non-voltage states, respectively. These are shared by all formulations.
AC Formulations
Anything specific to all AC formulations is included in the abstract class mp.nme_gizmo_ac, shown in Listing 17, which is a subclass of mp.nme_gizmo. Any concrete network model element class that inherits from mp.nme_gizmo_ac is also expected to be a subclass of a formulation class that inherits from mp.form_ac.
1classdef (Abstract) nme_gizmo_ac < mp.nme_gizmo% & mp.form_ac
2 methods
3 function obj = add_zvars(obj, nm, dm, idx)
4 tab = obj.data_model_element(dm).tab;
5 nk = obj.nk;
6 switch idx{:}
7 case 1
8 Zmax = ones(nk, 1);
9 Zr = tab.Zr1;
10 Zi = tab.Zi1;
11 case 2
12 Zmax = 2 * ones(nk, 1);
13 Zr = tab.Zr2;
14 Zi = tab.Zi2;
15 end
16 vname_r = sprintf('Zr%d_gizmo', idx{:});
17 vname_i = sprintf('Zi%d_gizmo', idx{:});
18 nm.add_var('zr', vname_r, nk, Zr, -Zmax, Zmax);
19 nm.add_var('zi', vname_i, nk, Zi, -Zmax, Zmax);
20 end
21
22 function obj = build_params(obj, nm, dm)
23 build_params@mp.nme_gizmo(obj, nm, dm); %% call parent
24 tab = obj.data_model_element(dm).tab;
25 nk = obj.nk;
26
27 %% collect parameters from data table
28 y1 = tab.Y1r + 1j * tab.Y1i;
29 y2 = tab.Y2r + 1j * tab.Y2i;
30 ll = tab.Lr + 1j * tab.Li;
31 ii = tab.Ir + 1j * tab.Ii;
32 m1 = tab.M1r + 1j * tab.M1i;
33 m2 = tab.M2r + 1j * tab.M2i;
34 nn = tab.Nr + 1j * tab.Ni;
35 ss = tab.Sr + 1j * tab.Si;
36 zz = zeros(nk, 1);
37
38 %% construct model parameters
39 j1 = (1:nk);
40 j2 = nk+j1;
41 j3 = nk+j2;
42 obj.Y = sparse( ...
43 [j1 j1 j1 j2 j2 j2 j3 j3 j3]', ...
44 [j1 j2 j3 j1 j2 j3 j1 j2 j3]', ...
45 [y1; zz; -y1; zz; y2; zz; -y1; zz; y1], 3*nk, 3*nk );
46 obj.L = sparse( ...
47 [j1 j1 j2 j2 j3 j3 ]', ...
48 [j1 j2 j1 j2 j1 j2 ]', ...
49 [zz; ll; zz; -ll; zz; zz], 3*nk, 2*nk );
50 obj.i = [-ii; ii; zz];
51 obj.M = sparse( ...
52 [j1 j1 j1 j2 j2 j2 j3 j3 j3]', ...
53 [j1 j2 j3 j1 j2 j3 j1 j2 j3]', ...
54 [m1; -m1; zz; -m1; m1; zz; zz; zz; m2], 3*nk, 3*nk );
55 obj.N = sparse( ...
56 [j1 j1 j2 j2 j3 j3 ]', ...
57 [j1 j2 j1 j2 j1 j2 ]', ...
58 [zz; zz; nn; zz; -nn; zz], 3*nk, 2*nk );
59 obj.s = [zz; -ss; ss];
60 end
61 end %% methods
62end %% classdef
The first method defined by mp.nme_gizmo_ac, namely add_zvars(), adds variables for the real and imaginary parts of the non-voltage state variables, \(\cvec{z}_1\) and \(\cvec{z}_2\), to the network model, constructing the initial values from the appropriate columns in the data table, and including predefined bounds. We arbitrarily define all gizmos such that their \(\cscal{z}\) variables, \(\cscal{z}_1\) and \(\cscal{z}_2\), obey \(-k \le \Re\{\cscal{z}_k\} \le k\) and \(-k \le \Im\{\cscal{z}_k\} \le k\). Note that the variable named Zr1_gizmo is vector containing the real part of \(\cscal{z}_1\) for all gizmos in the network. Because the voltage variable representation is different for cartesian and polar formulations, the implementation of add_vvars() is deferred to the formulation-specific subclasses below.
The second method, build_params(), first calls its parent to build the incidence matrices C and D, then constructs the standard AC model parameters from the data model. The AC model and its parameters are described in AC Formulations in the MATPOWER Developer’s Manual.
Recall that, if we omit the arbitrary nonlinear injection components, \(\Snln(\X)\) or \(\Inln(\X)\), the standard AC network model for any element type can be defined in terms of the six parameters in the equations below, namely \(\YY\), \(\LL\), \(\MM\), \(\NN\), \(\iv\), and \(\sv\).
For a single gizmo, based on Figure 2 and Table 2, these parameters would be defined as follows.
However, build_params() must build stacked versions of these matrix and vector parameters that include all \(n_k\) gizmos in the system. For the matrix parameters in (35) and (36), the stacking is done such that each scalar element is replaced by a corresponding \(n_k \times n_k\) diagonal matrix. For the vector parameters, each scalar element becomes an \(n_k \times 1\) vector.
AC Cartesian vs Polar Formulations
Once the parameters have been built, all of the differences between the cartesian and polar voltage formulations are handled automatically by inheriting from the appropriate formulation class. For the cartesian voltage formulation, we use mp.nme_gizmo_acc which inherits from mp.nme_gizmo_ac and mp.form_acc.
1classdef nme_gizmo_acc < mp.nme_gizmo_ac & mp.form_acc
2end
For the polar voltage formulation, we use mp.nme_gizmo_acp which inherits from mp.nme_gizmo_ac and mp.form_acp.
1classdef nme_gizmo_acp < mp.nme_gizmo_ac & mp.form_acp
2end
Mathematical Model Element
Since the gizmo does not introduce any new costs or gizmo-specific contraints, there is no need for an explicit mathematical model element for gizmos.
This is where you would also put any data_model_update() methods, but the gizmo does not implement any.
Note
The non-voltage state variables are not updated for the power flow, and in the OPF they have the hard-coded limits defined above.
Gizmo Extension
A MATPOWER extension that incorporates this new element can be found in lib/t/+mp/xt_gizmo.m.